
It is hard to summarize more than 20 years of intense research on cuprates and tens of thousands scientific articles, both theoretical and experimental! Hereafter, we will only emphasize the most significant properties of these compounds and why they are so hard to understand. We will also bring up some models that were suggested over the last few years to describe them.
The common point between all superconducting cuprates is the presence of two-dimensional square layers of copper and oxygen CuO2 separated by charge reservoir blocks as shown on the figure.
How can such a simple structure lead to such complicated physics? These layers have three combined particular properties that explain the originality of these materials:
When doping is equal to zero, which means all coppers are 2+, there is only one hole by copper, and the compound is then an insulator called a “charge transfer Mott insulator”. The magnets carried by electrons, called “spin”, then place themselves head-to-tail in a long-range order called “antiferromagnetic”.
Even in a normal metal, electrons are subjected to multiple interactions (interactions with the other electrons, with the atoms of the network). A mathematical treatment proves that when an electron is subjected to these interactions, it behaves exactly as a virtual electron subjected to no interaction, but the mass of which has changed. In some cases, the interactions are so powerful that the electric charge of this virtual electron can swap: we call the result a “hole”. This notion of electron and hole with a variable mass is a powerful theoretical tool because it enables to describe the electric properties of matter considering only interactions in matter.
 In most cuprates, the interactions are so powerful that the charge carriers are holes. When the number of oxygen ions or the nature of the other atoms is changed, the number of holes in CuO2 layers is modified. This number of additional holes is called “doping”. Whatever type of cuprates we are dealing with, the properties we observe when we change the doping are almost identical and seem to be rather universal. Above 0.05 additional holes by copper atom, the material stops being insulating and antiferromagnetic and becomes superconducting. Above its critical temperature Tc, it is a metal, in the sense that its resistivity in layers decreases when temperature decreases and has a relatively week value compared to semi-conductors and insulators.
In most cuprates, the interactions are so powerful that the charge carriers are holes. When the number of oxygen ions or the nature of the other atoms is changed, the number of holes in CuO2 layers is modified. This number of additional holes is called “doping”. Whatever type of cuprates we are dealing with, the properties we observe when we change the doping are almost identical and seem to be rather universal. Above 0.05 additional holes by copper atom, the material stops being insulating and antiferromagnetic and becomes superconducting. Above its critical temperature Tc, it is a metal, in the sense that its resistivity in layers decreases when temperature decreases and has a relatively week value compared to semi-conductors and insulators.
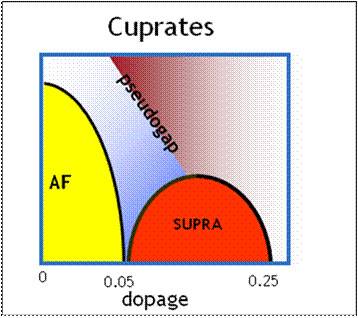 The critical temperature TC increases up to an optimal value, for a doping of 0.2, during the “underdoped” phase, then decreases during the “above doped” phase. The compound stops being superconducting above a doping of 0.3 additional holes by copper atom. Finally, another line in the phase diagram, called “pseudogap line”, defines another temperature scale in the underdoped zone, pointing out a progressive freeze in the low energy system properties. This line is distinct from the others because it does not represent an actual phase transition from one state to another. It is amazing that such a weak modification (0.05 to 0.15 additional charge carriers per atom) can transform an antiferromagnetic insulator in a superconductor presenting the highest critical temperature known to this day.
The critical temperature TC increases up to an optimal value, for a doping of 0.2, during the “underdoped” phase, then decreases during the “above doped” phase. The compound stops being superconducting above a doping of 0.3 additional holes by copper atom. Finally, another line in the phase diagram, called “pseudogap line”, defines another temperature scale in the underdoped zone, pointing out a progressive freeze in the low energy system properties. This line is distinct from the others because it does not represent an actual phase transition from one state to another. It is amazing that such a weak modification (0.05 to 0.15 additional charge carriers per atom) can transform an antiferromagnetic insulator in a superconductor presenting the highest critical temperature known to this day.
 What characterizes superconducting cuprates is their very high TC that can reach 138 K. In a conventional case of BCS theory, TC is hardly superior to a few dozen kelvins. However, as in the BCS theory, superconductivity also works thanks to Cooper pairs, as the measurements of Josephson effect and flux quantization have proved. The coherence length ξ characteristic of the extension of a Cooper pair is a few dozens angstrœms, which corresponds to 10 to 100 times less than in classical superconductors. The London penetration depth λ, characteristic of the penetration of a magnetic field in a superconductor, is however about the same size (0.1 to 1 µm) as in the BCS theory. In cuprates, there is a strong anisotropy of these properties that is caused by the two-dimensional structure of the layers. Finally, these unconventional superconductors are called type II superconductors, and their critical magnetic field BC2 (up to 100 teslas, typically) is much higher than in the case of a BCS theory.
What characterizes superconducting cuprates is their very high TC that can reach 138 K. In a conventional case of BCS theory, TC is hardly superior to a few dozen kelvins. However, as in the BCS theory, superconductivity also works thanks to Cooper pairs, as the measurements of Josephson effect and flux quantization have proved. The coherence length ξ characteristic of the extension of a Cooper pair is a few dozens angstrœms, which corresponds to 10 to 100 times less than in classical superconductors. The London penetration depth λ, characteristic of the penetration of a magnetic field in a superconductor, is however about the same size (0.1 to 1 µm) as in the BCS theory. In cuprates, there is a strong anisotropy of these properties that is caused by the two-dimensional structure of the layers. Finally, these unconventional superconductors are called type II superconductors, and their critical magnetic field BC2 (up to 100 teslas, typically) is much higher than in the case of a BCS theory.
 In a BCS superconductor, the superconducting order parameter Δ (the gap) is characterized by a type s isotropic symmetry, and there is a universal relation between TC and Δ : 2Δ=3,5kBTC. In cuprates, it is a type d(x2-y2) anisotropic symmetry. This kind of symmetry means that on the one hand, the order parameter swaps sign according to its direction and on the other hand that there are directions for which the gap is cancelled. This anisotropy does not change much with doping and seems to be present in the entire phase diagram and in all the studied compounds. In case of optimum doping, the maximum gap amplitude varies according to TC as in the BCS theory. On the contrary, Dmax does not vary according to TC depending on doping but decreases when doping increases. In an underdoped compound, the Δmax/kBTC ratio can be 10 times higher than the expected value in a BCS model with a weak-coupling constant. A simple BCS explanation can no longer explain superconductivity in these materials.
In a BCS superconductor, the superconducting order parameter Δ (the gap) is characterized by a type s isotropic symmetry, and there is a universal relation between TC and Δ : 2Δ=3,5kBTC. In cuprates, it is a type d(x2-y2) anisotropic symmetry. This kind of symmetry means that on the one hand, the order parameter swaps sign according to its direction and on the other hand that there are directions for which the gap is cancelled. This anisotropy does not change much with doping and seems to be present in the entire phase diagram and in all the studied compounds. In case of optimum doping, the maximum gap amplitude varies according to TC as in the BCS theory. On the contrary, Dmax does not vary according to TC depending on doping but decreases when doping increases. In an underdoped compound, the Δmax/kBTC ratio can be 10 times higher than the expected value in a BCS model with a weak-coupling constant. A simple BCS explanation can no longer explain superconductivity in these materials.
To summarize, the superconducting state presents many characteristics that are very different from the BCS classical superconductors: anisotropic symmetry, gap not depending on TC, magnetic modes, etc. However, some of these properties can be explained with an adjusted BCS theory, especially as far as residual quasiparticles are concerned.
Above TC, when the material is no longer superconducting, its metal state is also unusual and not well understood. For instance, at optimum doping, when TC is the highest, all the properties of the system present a highly abnormal behaviour compared to a normal metal: electrons with a very unusual energy (called “self-energy”), a resistance varying linearly according to the temperature (while it should be varying according to the square of temperature at low temperature), and magnetic fluctuations that should not exist. The optimal doping state is hence difficult to describe in terms of metal (physicists call it a non “Fermi liquid”), whether it be its magnetic properties or its charge. It is also difficult to describe the exact nature of the carriers involved.
Things get worse when getting close to the insulating zone, in the “underdoped” state. In this state, a new boundary called “pseudogap” appears, under which a progressive freeze in the system answers to any excitation appears, such as a magnetic field for instance. Knowing whether this line has something to do with superconductivity and understanding its exact meaning is one of today’s big issues.
 Many models try to predict the unusual properties of cuprates, but none has, to this day, managed to give a clear and coherent explanation to the entire phase diagram and to all the experimental results. The main difficulty comes from the microscopic starting point: trying to solve the model that best describes the movement of electrons in CuO2 layers, called “two-dimensional Hubbard model”. However, some models try and explain the origin of superconductivity. Let us quote some of them:
Many models try to predict the unusual properties of cuprates, but none has, to this day, managed to give a clear and coherent explanation to the entire phase diagram and to all the experimental results. The main difficulty comes from the microscopic starting point: trying to solve the model that best describes the movement of electrons in CuO2 layers, called “two-dimensional Hubbard model”. However, some models try and explain the origin of superconductivity. Let us quote some of them:
An adaptation of the BCS model with particular atom vibrations (“phonons”) in these perovskites, focusing on the role of oxygens around coppers;
Models that explain superconductivity thanks to the key role played by magnetism: theories according to which the electron spins pair antiferromagnetically but in a dynamic way (this is called “spin fluctuation”), pairing and unpairing through time, or other theories according to which spins make some sorts of antiferromagnetically orderly bags (“spin bags”), or even alternating magnetic and superconducting stripes;
Models emphasizing the role of “Van Hove singularity”, some sort of accident in the energetic characteristics of electrons that would enable TC to increase;
Models linked to the very shape of the phase diagram and what we call “quantum critical points”;
Models that postulate the existence of a hidden order in the pseudogap phase: the existence of small “orbital” electric currents stuck in orderly layers, for instance, or spin density waves;
“RVB” models, where the electron spins would form original quantum states and could “live” free from the electron charge (spinons and holons);
Models according to which the pseudogap actually indicates the emergence of preformed Cooper pairs, true superconductivity appearing at a lower temperature, when all pairs become coherent;
Etc.
This long list shows how cuprates have been highly stimulating for physicists of condensed matter and have enabled the development of new concepts and new original types of experiments that have since been conducted on other materials in order to study different physical domains.
